EV in Sanma, a small step towards better discourse in Mahjong.

Hey. Lovepon here *Insert YouTube-Essayist-esque wave to the camera*. I just looked into my blog folder and discovered an unpublished blog from last year April that was titled “Caring about things that actually matter”, to my surprise, the blog was completely empty, void of anything but the title. Hmm… Yeah I didn’t do a very good job of that back then, and not doing a very good job of it now, as I am about to write a blog on Riichi Mahjong’s Sanma.
Sanma, the lesser respected three player version of Riichi Mahjong, was not something I was aware of until I was a few months into this rabbit hole. Long story short, I was playing the 4 player Riichi Mahjong for the sake of writing my Furry novel, then got bored of that and got hooked on Sanma instead. The only way to justify my addiction was to implement Sanma as a part of the pointless story I am trying to craft. I guess it wasn’t entirely pointless because one person read it and she is still alive.
However, that story is now done, so is the story of me testing how good I am at the game in Mahjong Soul. After 1.5K games, I am now stuck in a cycle of being a player who is “too good for Master 2” and “too mediocre to stay in Master 3”. Repeatedly playing the game again seems pointless since I don’t think I can “intuitively” transform myself into a good player by just hoping that somehow after playing 5K games, I would make decisions that give me a 37% 1st rate and 27% 3rd rate that would be enough to make myself a Saint level player.
Speaking of “Saint” rank, ranks in games are pointless to achieve, everyone knows it to an extent. Lots of people in this world walk with nothing to their name, I am one of them. And so, I can’t fully get rid of this innate “strive for greatness”, the one last thing that make me interested in this game (Lie). But I am less interested in actual improvement as opposed to the “roleplay” of pretending that I am trying to discover something special.

Thank you Puapka for drawing the cover of my book. Here is its webcomic, Slowpoke
“This is good because Yes… bad because no.”
WWYD, short for “What Would You Do?”, is a phenomenon where a user post a picture of their game with a difficult decision, and ask the rest of the community what would they do, and their rationale behind it.
I posted a WWYD few times and I received a few responses before from top players in Celestial rank, equivalent of Master player in LoL, giving insights such as: “You should fold because the chance of you winning is low”, “You should push because you lack enough safe tiles early into the game.”
The way people talk about Mahjong seems to be based on vague concepts brought up by Japanese pros in books. They are good advice, they work, following them will make you win more. Studying the VODs to see what good players do, and see how these advices gets implemented into the actual matches the good players play. Play consciously, play while healthy, don’t tilt, and take notes.
I am not too interested in proving myself with my rank, but moreso interested in being able to discuss Mahjong, something I dedicated far too much time into, in a more “satisfying way”. Less vague “yeah maybe win rate high, maybe close, eh…” and more “I did a calculation just now and based on the math, X decision is better than Y.”
The problem is that Mahjong is very hard to solve with math that is comprehensible to a lowly, feet licking liberal art major graduate such as myself. Another “problem” is that companies are already looking into creating an AI specifically for Sanma, a tool far smarter and stronger than a human mind like mine will ever be. And so the question is, is there even a point to me looking to calculate the odds for Mahjong myself?
Not really but I don’t feel like doing my taxes this Sunday.
Calculating Mahjong EV, Pt.1/(?)

Here is a WWYD, except let’s pretend that Right Villain didn’t Riichi, and that both opponents will proceed to Fold perfectly without dealing in after you commit to Riichi right then. Under the “digital” assumption of the unrevealed tiles, not accounting for Pei, not accounting for Kan, and Rinshan Kaihou, let’s also assume every tile not in our winning hand can be an extra Ura Dora. What would be the EV of your Riichi?
Oh boy… That is a lot of things not accounted for, and what is the point of solving this oddly specific question? Well… This “conveniently crafted” question that I made “some” progress in… Because the more difficult and useful questions require a lot more work. I would love to solve situations involve Chases and how points differential influence the kinds of lines a player must take to get a higher rank in the future.
Going back to the actual question. At first, I thought… “This problem is impossible to solve with a decision tree.” Luckily, turns out this Card Game Calculator is a very helpful tool that introduced me to the concept of Hypergeometric Distribution, then I used this Guide to implement that into a spreadsheet.
The method used is basically: What is the chance that there is 0-4 tiles in the dead wall or opponent’s hand? Which would always be 42 in this particular situation as your opponent has 13 * 2 = 26 tiles in hand, 14 tiles in dead wall, and they will draw 2 more tiles after you. Then determine the rate that you will fail to Tsumo if there are 1-4 tiles in the draw pile, and calculate the Tsumo Rate based on that. Finally, to see how high your score can get, calculate the basic Ippatsu and Uradora Rate, and then see in how many % of scenarios would you get X Han based on that if you Tsumo.
Here are some cool tables and fun facts about this scenario:

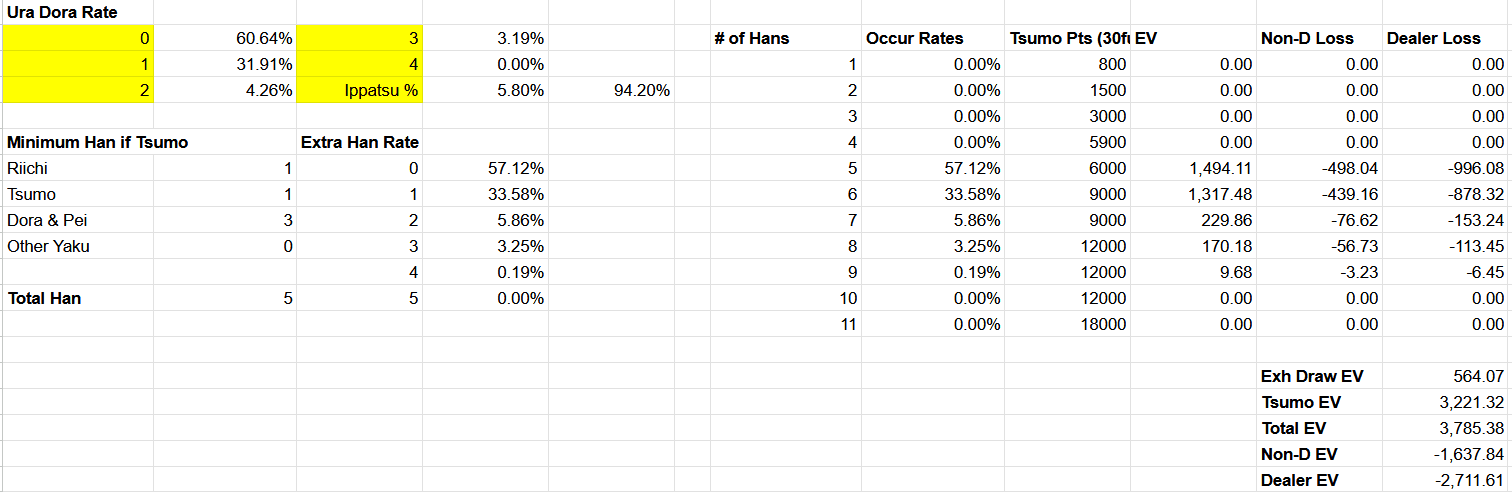
- You have a 43.6% chance of winning via Tsumo in the above situation.
- When you Riichi with a bad wait in the scenario above, there is a 13% chance that your opponent already hold all the 7s you have.
- If there are 4 tiles left that can be drawn from the remaining 29 tiles, you would have 82.56% chance of winning via Tsumo. However… There is also only a 2.03% chance that there are 4 in the draw pile.
- Ura Dora rate depends on your hand composition. The typical hand above has a 39.36%% chance of hitting at least 1 Ura, and a 3.25% chance of Ura 3!
- After you Riichi, there is a 57.3% chance of you both missing the Ippatsu (5.8%) and missing an Ura Dora (60.64%), which would result in your hand value being just 5 Han Mangan rather than a Haneman. 39.44% chance that you would get a Haneman, and a slim 3.44% chance for Baiman.
With everything in mind. The EV for our hero here is +3785 points, while the dealer has to pay out an average of -2712 points for the loss and non-dealer pays out -1638. They don’t quite add up because 1000 point will be in the middle in case of exhaustive draw, which is -564 points. If Pei is added to the conversation, the points won/loss would be slightly higher for the hero I would imagine as it will bump up the Han # to 6 Han Minimum even without Ura.
Pesky Pei…
Pei, the dopamine tile in game is also the headache tile for math noobs like I....It’s hard to implement it into the calculation. They give the player an extra draw, an extra Han, a tiny chance of miracle Rinshan Kaihou, and it mess up the rhythm of the entire game as it will result in one player getting 1 fewer draw.
Not sure how am I supposed to implement Pei into this model yet, what’s harder is implementing scenarios where another player is in Riichi, or even “chaotic” cases where everyone is attempting to do something meaningful… Well, I am looking forward to do more of this and hopefully solve more meaningful questions in the future. If someone else wants to collaborate or solve this dire problem themselves, I would be very happy.